Index set

In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set. The indexing consists of a surjective function from J onto A and the indexed collection is typically called an (indexed) family, often written as (A_j)_j∈J.

In computational complexity theory and cryptography, an index set is a set for which there exists an algorithm I that can sample the set efficiently; i.e., on input 1ⁿ, I can efficiently select a poly(n)-bit long element from the set. ^[1]

Examples

An enumeration of a set $S$ gives an index set 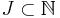$J \sub \mathbb{N}$ , where $f : J \to S$ is the particular enumeration of $S$ .

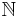Any countably infinite set can be indexed by $\mathbb{N}$ .

For 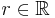$r \in \mathbb{R}$ , the indicator function on $r$ is the function 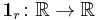$\mathbf{1}_r\colon \mathbb{R} \rarr \mathbb{R}$ given by

$\mathbf{1}_r (x)�:= \begin{cases} 0, & \mbox{if } x \ne r \\ 1, & \mbox{if } x = r. \end{cases}$

The set of all the 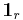$\mathbf{1}_r$ functions is an uncountable set indexed by $\mathbb{R}$ .

References

^ Goldreich, Oded (2001). Foundations of Cryptography: Volume 1, Basic Tools. Cambridge University Press. ISBN 0-521-79172-3.

Index set

Examples

References

See also